 CERCLE
CERCLE
 CORONA CIRCULAR
CORONA CIRCULAR
 SECTOR CIRCULAR
SECTOR CIRCULAR
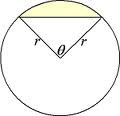 SEGMENT CIRCULAR
Acercle= π • r2
Asector circular=(π•r2 •α) : 360
Asegment circular= Asector – Atriangle OAB
Acorona circular= π(R2 – r2)
SEGMENT CIRCULAR
Acercle= π • r2
Asector circular=(π•r2 •α) : 360
Asegment circular= Asector – Atriangle OAB
Acorona circular= π(R2 – r2)
 CERCLE
CERCLE
 CORONA CIRCULAR
CORONA CIRCULAR
 SECTOR CIRCULAR
SECTOR CIRCULAR
 SEGMENT CIRCULAR
Acercle= π • r2
Asector circular=(π•r2 •α) : 360
Asegment circular= Asector – Atriangle OAB
Acorona circular= π(R2 – r2)
SEGMENT CIRCULAR
Acercle= π • r2
Asector circular=(π•r2 •α) : 360
Asegment circular= Asector – Atriangle OAB
Acorona circular= π(R2 – r2)
3.3. Volum del con i la piràmideDe manera experimental, podem comprovar que el volum d’una piràmide és la tercera part del volum d’un prisma amb la mateixa àrea de base i idèntica altura.
VPiràmide = 1/3VPrisma à VPiràmide = 1/3 (ABase · h)
De manera anàloga, podem calcular el volum d’un con relacionant-lo amb el volum d’u n cilindre amb la mateixa base i altura.
VCon = 1/3 VCilindre à VCon = 1/3 (TTr2 · h)
|
 |
 |
||||||
 |
|||||||
 |
|||||||
 |
|||
 |
|||
 |
|||
 |
|||
 |
 |
||||||
 |
|||||||
 |
|||||||
 |
|||
 |
|||
 |
|||
 |
|||
Fòrmula de l’àrea
|
|||
Cercle: Superficie plana que es trova a dintre
d’una circumferència.
|
|
A= πr2
|
|
Sector circular: és la porció d'un cercle reclòs per dos radis
i un arc.
|  | A=r·r·àngle donat/ 360
|
|
Segment circular: és la
superfícieplana delimitada per una corda de circumferència i l’arc que li correspon |
 |
A= Asector-Atriangle
|
|
Corona circular: superfície continguda entre
dues circumferències concèntriques.
|
A=π(R2-r2)
|
||